Author: Eleanor Duckworth
Published in: Harvard Educational Review
Published: 02/01/1991
Source URI: http://pp.mspnet.org/index.cfm/12520
Abstract
Eleanor Duckworth,
"Twenty-four, Forty-two, and I Love You: Keeping
It Complex,"
Harvard Educational Review, 61:1 (February,
1991), pp. 1-24. Copyright © 1991 by the President and Fellows of
Harvard College. All rights reserved. Used with permission.
Posted to Site: 12/09/2005
ELEANOR DUCKWORTH
Harvard Graduate School of Education and University of Ottawa
In this article, Eleanor Duckworth focuses on the nature of understanding by leading the reader through the process of extended clinical interviewing. Duckworth describes some of her own explorations of science and how those experiences showed her what learning could be like. Those experiences included working with "a highly imaginative bunch of scientists and teachers of science" while developing the Elementary Science Study, a curriculum development program. As she describes it, Duckworth 'got hooked' on the excitement of learning and has been an educator ever since, working to develop engaging learning experiences for both teachers and students. This article continues her effort to do just that, with lengthy descriptions of her own and her students' struggles—and enjoyment—as they attempt to understand and define various phenomena. And with that, she opens the discussion of "keeping it complex."
In my entire life as a student, I remember only twice being given the opportunity to come up with my own ideas, a fact I consider typical and terrible. I would like to start this article by telling how I came to realize that schooling could be different from what I had experienced.
Figuring Out My Own Ideas
After my university studies, I joined the Elementary Science Study, a curriculum development program. I had been hired because of my background with Piaget, studying how science and math ideas develop in children, and had no formal training in either education or science. While the first of these lacks was probably a liability, the second turned out to be a great boon. I was working with a highly imaginative bunch of scientists and teachers of science, all trying to put together their favorite kinds of experience to entice children. Because I was innocent in science I made a great "sample child" for my colleagues, and I spent a lot of time exploring the materials and the issues that they came up with. Of the many areas I explored, three seemingly unrelated ones came together in a way that showed me what learning could be like. I got hooked and have been an educator ever since, trying to develop learning experiences of that sort for every child and every teacher. It was the first time—with two exceptions mentioned in the opening sentence—that I got excited about my own ideas. I had been excited about ideas before, but they had always been somebody else's ideas. My struggle had always been to get in on what I thought somebody else knew and knew to be important. This was the first time that I had a sense of what it was like to pay attention to my own ideas.
It is, of course, exhilarating to find that your own ideas can lead you somewhere. Few feelings are likely to be more effective in getting you to keep on thinking about things on your own. I would like to focus here, though, not so much on my feelings as on the nature of my understanding.
One team of colleagues was developing ways to study balances. They posed problems with a simple balance that consisted of a strip of pegboard resting on a rounded support with metal washers as weights. In each case, they started with the balance in equilibrium, horizontal. Then, holding the balance, they moved one or more weights and asked me to adjust other weights so that when they let go, the balance arm would remain horizontal (see Elementary Science Study, 1967b).
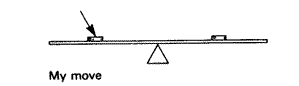
For example, they set up a relatively easy problem with the balance, as shown here:

Where could I add one washer, so the board would stay balanced? My solution was as follows:
They then gave me a problem that I found more difficult: they presented me with the board balanced with one washer on one side and two washers stacked on the other side, but closer to the middle. If they moved the single washer a certain distance to the right, how could I move just one of the other two washers, so the board would still balance?

I found that this solution worked:
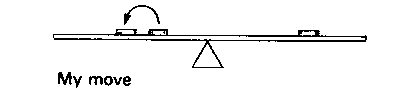
Through this example and others similar to it, I found that it did not seem to matter where the washers started; I just had to move one of them the same distance the original had been moved on the other side, but in the opposite direction.
My grand triumph was the following problem. To start with, they put three washers in a pile on one side so as to balance one on the other:
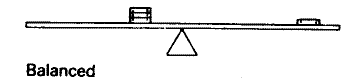
Then they moved the single one a long way—practically to the center. Again, how could I move just one of the others so it would still balance?
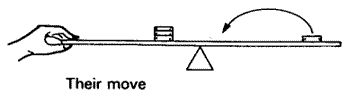
Well, I knew by now that I should try to move it just as far in the opposite direction, but there was no room. I ran into the middle almost right away. So what should I do? Move it in the same direction? That didn't seem right. Move it as far as I could towards the middle—just barely short of the middle? I thought I might try that. But the one I decided to try was my first idea—moving the washer in the opposite direction, even though it meant crossing the middle.
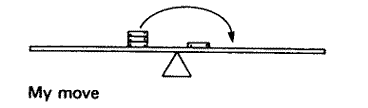
It felt to me like a very daring move And it worked! The rule worked, even across the middle. I remember saying to my colleagues at the time that I felt like Helen Keller.
I did not stop then. Among other things, I tried designing balances myself, and eventually even figured out what the differences were between a balance and a seesaw that accounted for the fact that the balance with nothing on it is horizontal, while a seesaw with nobody on it always has one end up in the air.
A second group was working on a study of what they called Gases and "Airs" (Elementary Science Study, 1967a). The tight sequence of reasoning demanded by this unit turned out not to work very well with elementary school children, but the unit did entail a wonderful variety of experiences that, for me, gave substance to what gases and airs are. It started from a close and critical look at the classic school science lab demonstration of burning a candle in a tube inverted over water: the water rises, the candle goes out, and one has "proven" that the atmosphere is 20 percent oxygen. But, there are some problems, as my colleagues pointed out. For one thing, the water doesn't rise gradually as the candle burns; it rises suddenly after the flame is out. If it were gradually using up the oxygen, wouldn't it gradually rise? Another problem: the amount that it rises may indeed average about 20 percent, but it varies widely; in contrast, when wet steel wool is wedged into a tube above water and left to rust overnight, the water rises exactly the same amount in each tube.

| Water rise after 4 candles burned | Water rise with steelwool overnight |
The "demonstration" with a burning candle turns out to be a hoax, based on a totally different phenomenon. The candle actually goes out long before all the oxygen is used up (for various reasons). While the candle burns, it heats the air so that the air expands; some of it leaves the tube, bubbling out through the water in the dish. While the remaining air cools, the water rises to take the place of the air that bubbled out. As one who had been taken in by that demonstration in my own schooling, I was fascinated to explore the more complex relationships that had been covered up by it. To begin with, I was intrigued by the idea of different kinds of "airs" easily available to us: air that a candle had burned in; air that steel wool had rusted in; lung air; room air; air that seeds had sprouted in. Could a candle burn in the steel wool air? Would another rusting steel wool ball pull up the same amount of water in steel wool air? Would seeds sprout in candle air?
I became very good at putting into a tube whatever kind of air I wanted to. Using a syringe, I could take air from any tube and put it into another tube that had no air in it (by virtue of being full of water). Bubbles came to be real things filled with some one kind of air—room air, lung air, steel wool air, or other. Putting an Alka Seltzer tablet under the lip of a water-filled tube, for example, did this:

and I had a tube full of Alka Seltzer air.
I came to imagine the inverse of filing any container with liquid. As long as your container has no other liquid in it already, you can put it straight under the dripping liquid, and you'll capture all that is falling right over the opening In the inverse, as in the case of some escaping Alka Seltzer air, you could think of it this way:
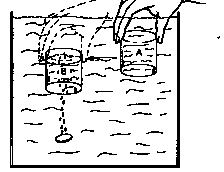
In a bucket of water, move a water-filled jar over the bubbles, and you will collect the escaping Alka Seltzer air.
This is not, I hasten to point out, intended as a practical example: I've never happened to be holding a water-filled jar upside down in a bucket of water- when an Alka Seltzer tablet dropped into the bucket. But conceptually it helped me a lot: an "air" was for me as real as a liquid.
A third area that I explored originated in my attempts to build on my Piaget background. I thought of trying to find some situations for young children in which a certain order was maintained in spite of some striking change. It occurred to me to use the constant ordering of liquids floating on each other in a tube. Though the idea had less mileage in it for little children than I had thought it might, it did have some value (see Duckworth, 1964). More importantly for my education, however, it led me into a long series of explorations with liquids, starting with trying to make as many floating layers as I could in one tube. If I did not shake the tube, I could manage about six layers, and I experimented with dyes to keep the layers distinguishable. I expanded my horizons to include solid pieces—seeds, bits of plastic, bits of wood, bits of food. I don't recall any of these specifics, but a radish seed, say, would fall through three layers and sit on the fourth—and every radish seed would do that. One kind of plastic would sit on the second layer, another kind would fall through four, and so on. Some material (I do not now remember what, and it took me a long time to find this material) stopped at the top of the top surface and floated there.
I also tried to mix alcohol and water so that the resulting liquid would have exactly the same density as the salad oil I was working with—to see what would happen when neither liquid would necessarily float on top of the other. Would I be able to make stripes with them? Or would they stand side by side, with a vertical separation? Or what? I found that the oil always formed itself into a single enormous sphere in the middle of the water-alcohol liquid; and that this sphere always moved slowly either to the top or to the bottom of the water-alcohol liquid. No matter how delicately I added one drop of wafer or of alcohol, I could never get the sphere of oil to float right in the middle—it was always either just heavier or just lighter. (These explorations came back in my own teaching more than ten years later; see Duckworth, 1986.)
Six or eight months after I started learning science like this, someone presented a puzzle that happened to draw on the three areas I had been exploring. I think I was the only person around at the time who put together the right prediction.
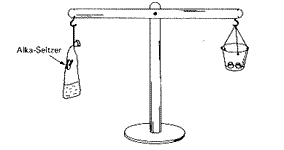
On the left-hand side of this balance is a plastic bag sealed airtight; an Alka Seltzer tablet is stuck in a piece of plasticene near the top, and some water is in the bottom. On the right-hand side is just enough weight to balance the arm. The question is, what will happen to the balance of the arm if the bag is shaken, and the tablet falls into the water?
Most of the people present knew that when the tablet fell into the water, a lot of "Alka Seltzer air" would be formed and the bag would fill out. Some people thought that the arm would remain level, because the same matter that was in the bag to start with was still in it at the end, even if in a different form, so the weight would not change at all. Others thought that the left side would go down, because Alka Seltzer air (being, as they knew, carbon dioxide) is heavier than room air. My prediction, which, in fact, turned out to be the case, was that the left side would go up, because the filled-out bag would take up more space, while adding no more weight, thus being more buoyant in the surrounding sea of air.
I believe that it was because I started from my own ideas and found my own ways into these parts of the world that my understanding of balances, "airs," and floating belonged so thoroughly to me. Notice the difference between what usually happens in formal education—presenting the simplest, neatest explanation of "the law of moments," "the composition of the atmosphere," "density," "buoyancy," or whatever; and my experience of being enticed with the funny, frustrating, intriguing, unpredictable complexities of the world around me. Instead of disassociating myself from my own interests in my struggle to find out what whoever was supposed to "know" might have understood by the word "buoyancy," my learning was based on my own connections, within the idiosyncrasies of my own system of thoughts. The very complexities of the subject matters enabled me to connect with them, made them accessible, and the integrity of my own ideas enabled me to retrieve those connections when they could help me understand a new situation.
Lisa Schneier (1990) describes the relationship between complexity and accessibility in this way:
[W]e organize subject matter into a neat series of steps which assumes a profound uniformity among students. We sand away at the interesting edges of subject matter until it is so free from its natural complexities, so neat, that there is not a crevice left as an opening. All that is left is to hand it to them, scrubbed and smooth, so that they can view it as outsiders. (p. 4)
The experience of my science explorations was the exact opposite.
The Universe in a Sentence
My favorite radio show is "A Hitchhiker's Guide to the Galaxy." In one episode, a computer is built expressly for the purpose of answering the question, "What is the meaning of life, the universe, and everything?" When it is ready, they ask it if it can answer that question. It says, yes, it can, but that it will take, as I recall, seven million years. They say, "Well, OK, go to it." Seven million years later, whoever is around goes to learn the answer. The computer says that it does have the answer, but that it might be a little disappointing. "No, no," they say, "go ahead, what is it?" "Forty-two," the computer says.
Who knows? Maybe forty-two is the answer. But such an answer is of no more help to us than no answer at all. It does not speak to our level of interaction with the mysteries of our existence.
Note the parallels with the following story from Lisa Schneier's class in an urban high school:
It had been a lively class, with the various Juliets taking turns standing on a table and the Romeos making elaborate and often comical gestures as they stood below. . . . A group of ninth graders and I were working on a scene from Romeo and Juliet. They had chosen to read the balcony scene aloud and were acting it out, taking turns with the parts. They took the difficult language and its foreign style into stride, at times staying true to the text and at others replacing or skipping words and phrases. It was clear as they spoke that at points the words held meaning for them and at others they hadn't a clue as to what it was that they were reading. But we didn't stop much for discussion; the students were enjoying this kind of involvement with each other, and there was a momentum in the reading that I didn't want to interrupt.
But our last Romeo of the day finally did interrupt it. We had started the scene again to give more readers a turn, and he had begun to wade through his first speech. In the midst of it, he broke off, shook his head impatiently, and turned to me. "He loves her. That's what he's saying. So why all that other stuff? Why not just say it? I love you! (to the current Juliet). There!" And then in a memorable tone, a mixture of humor, frustration, and holiest confusion: "Why can't he just say what he means?" (Schneier, 1990, pp. 1-2)
Why doesn't Shakespeare just say what he means? Of course that's what he is doing: "what he means" is complex. The words he chooses are the best he can choose to say what he wants to say. Poems and stories and paintings and dance and music are not just fancy ways of saying what could be said in a sentence. "I love you" does not quite express everything that Shakespeare meant, just as "forty-two" does not quite substitute for living our lives. There is a parallel here between a poet and a teacher: the universe is complex; science is complex; the poet's thoughts and feelings are complex "Forty-two" doesn't do the trick. Neither does "buoyancy." Nor, in this case, does "I love you."
In this spirit, when studying a poem with a class, I start by asking students what they notice—an invitation to keep every complexity of the poem under consideration. People notice very different things, and almost each thing noticed leads to a question or another thought. Putting together what everyone notices and returning to the poem to try to look for answers to the questions leads to an understanding of the poem that is greatly expanded for each of us. Take, for instance, this Frost poem:
DESIGN
I found a dimpled spider, fat and white,
On a white heal-all, holding up a moth
Like a white piece of rigid satin cloth—
Assorted characters of death and blight
Mixed ready to begin the morning right,
Like the ingredients of a witches' broth—
A snow-drop spider, a flower like froth,
And dead wings carried like a paper kite.What had that flower to do with being white,
The wayside blue and innocent heal-all?
What brought the kindred spider to that height,
Then steered the white moth thither in the night?
What but design of darkness to appall?—
If design govern in a thing so small.1
Somebody will notice that there is a lot of white. Somebody will mention the rhyme scheme, or will imitate the rhythm. Somebody will mention that the first part of the poem seems to present a picture, and the second half seems to ask questions about it. Different people point out different possible plays on words: kindred and dreadful kin; appall and a funeral pall; a paper kite and a bird kite; morning right and morning rite; morning and mourning. Different people have different thoughts about whether the darkness is that which appalls, or that which is appalled. Arguments develop about why the flower is described as white in the first line, and blue in the ninth. This is a bare beginning. A group of adults can easily go for more than an hour with increasing interest, and everybody's initial understanding is expanded by hearing from others.2
I have always been frightened by being asked: "What is the meaning of this poem?" My reaction is, "How could I know? I'm no good with poems!" But it is easy for me to point out something that I notice about it, and in turn to listen to what other people notice, about it, and to figure out whether I think that what they say makes sense, and why, and what other thoughts their ideas provoke in me. Many students have feelings similar to these. One in particular said that she had determined when we started discussing the poem that she would not say a word, knowing nothing about poems and feeling scared by them. But as she heard the various things that people were saying, her own thoughts developed, and she finally couldn't contain herself, so much did she have to say and so strongly did she feel about it. One student referred to himself as a "poem-phobe," which prompted another student to say, "If Frost had been able to put what he had to say into a sentence, he would have. So don't worry that you can't."
I recognized that this was the same thought I had about the accessibility of science. It is in acknowledging the complexity of the poem, not "sand[ing] away at the interesting edges," to use Schneier's words, that we render it accessible. Our understanding seeks to do justice to the complexity that the poet sought to render, and by the same token it belongs to us. Just as the poet seeks to present his thoughts and feelings in all their complexity, and in so doing opens a multiplicity of paths into his meaning, likewise a teacher who presents a subject matter in all its complexity makes it more accessible by opening a multiplicity of paths into it.
"I Know There Are Twenty-four"
I ask students to do the following: Take a fistful of four different kinds of markers (four colors of paper clips or four kinds of dried beans, for example) to represent four children who are going to the movies. Lay out the different arrangements in which they can sit in four adjacent seats. Some students ask, "Do I really have to do this? I know there are twenty-four." And I say, yes, you really have to; the question isn't how many arrangements, the question is what are the arrangements—each of them. (It happens, not infrequently, that someone who has impatiently affirmed that there will be twenty-four, because he or she knows a formula, has trouble generating the actual arrangements—which strikes me as not too different from knowing that the meaning of life is forty-two.) And the question behind that is, when you think you have laid out all the arrangements, how could you convince yourself or anybody else that you don't have any repeats, and that you are not missing any? I urge the reader to try this before continuing, and to see what system she or he comes up with.
Most non-math people start this exercise more or less randomly, but many systems emerge when they think about whether they have generated all the possible arrangements. In what follows I will present some of these systems.
Some people make diagonals, such as with the P in the following arrangements:
PBLM
MPBL
LMPB
BLMP
This could be called the 'revolving' system, where the last letter to the right revolves around to appear on the left, and everything moves over one. This looks systematic and promising, but when they follow this rule to the fifth step, it turns out to be a repeat of the first (PBLM). So they have to side-step, and think about how to find the various different possible starting points.
Another system which keeps P on the diagonal is the "squeeze between" system:
PBLM
BPLM
BLPM
BLMP
Move P to the right by squeezing it in between the next two letters. Again, the question arises about what to do after the fourth.
You could reinterpret that system to be not "squeeze between" but "exchange": Keep P moving on the diagonal by exchanging it with whatever letter is in the place where it will be moving. That explains the four above, and allows you to keep going:
PLMB
LPMB
LMPB
LMBP
PMBL
MPBL
MBPL
MBLP
At this point, after twelve arrangements, we get back to the starting point. Is that, then, all there are? Is there a reason to think that this system would have generated all we could possibly get? Is there a reason to think it is inadequate? Or can't we tell anything about it at all?
Not all approaches use diagonals. For the next ones I will limit the discussion to three children in three seats in order to write out fewer arrangements.
Many people, as a system starts to emerge, lay out something like this:
LMB
LBM
MLB
By this time they have an idea about what they will put next, and most think that their idea is the only sensible, systematic possibility. The first surprise is that there are two different, almost equally popular, next moves:
MBL or BLM
And the two completed lists would look like this:
I
LMB
LBM
MLB
MBL
BLM
BML
II
LMB
LBM
MLH
HLM
MBL
BML
The system on the left started with two L's in the first position, then put two M's in the first position, and then two B's The system on the right started with the L's in the first position, then moved the L's to the second position, and then to the last position. In both cases, people can say, "Once I have one position filled, there are only two ways to fill the other two, so these are the only possible six ways for three children to sit." They are two very different systems, and yet they could up with the same exact arrangements.
Playing this out with four children and four seats, using, for example, system 1, would give this result:
PLMB
PLBM
PMLB
PMBL
PBLM
PBML
There would be six different arrangements with P in the first position. There would, therefore, be six ways to put each of the four letters in the first position; that is, four times six ways altogether. (Playing out system II above, P would end up in each position six times—again, four times six ways altogether.)
One nine-year-old—no math whiz, he—after placing a few arrangements according to no system that I could see, started to make new ones by reversing pairs in the ones he already had. (From PLBM, say, he might make PBLM; or from MLPB he might make LMPB.) He worked slowly, and for a long time he would make a new arrangement and then check to see whether he already had it rather than generate a new one from some overall system he had in his mind. After a long time, though (he worked at this for close to an hour), and as he explained to me what he was doing, a system emerged; he started to know how to look for ones that were missing and to fill in the gaps. It was a system that was totally new to me. He never articulated it as clearly as I am about to here, but essentially his system was as follows.
Start with one block, let's say P, and pair it up with each of the other blocks in turn. Let's start with the pair PL; put them in the middle, and put the two remaining blocks at either end. Then reverse the two on the ends. Then reverse the originals (PL becomes LP) and repeat. Then put the end-ones in the middle and the middle-ones at the ends and start over.
BPLM
MPLB
BLPM
MLPB
PBML
LBMP
PMBL
LMBP
Now we have eight. Starting with PM gives us another eight and starting with PB gives us eight more. This way you get three times eight instead of four times six. Is there any reason that this system is a convincing one? When you've started with P and each of the other letters and done all the rearrangements as described, is there any reason to think that you would necessarily hit all the possibilities?
I could go on. Looking for relationships among the systems enhances our understanding even more: What is the relationship between a system that has four variations of six positions and a system that has three variations of eight positions? The point is that the more you look at this question, the more ways there are to see it. "Twenty-four" is a sadly impoverished version of all that can be understood about it. Just as with the poem, each different way of thinking about it illuminates all of the others—a wonderful pay-off for allowing for the complexities of the matter. Note that in this math problem, as with the poem, individuals tend to think that their way is the one way to look at it, unless they are in a social context where other possibilities are presented; then it is not a matter of replacing their point of view, but of enhancing it.
Of course, many people raise for themselves the question of arrangements of five children, and work out a formula that applies to any number—a formula which, then, represents their understanding instead of substituting for it.
One further comment: Another nine-year-old pointed out to me that, once he had laid out all the arrangements (and he came up with twenty-four), if he removed the first item from all of them, the twenty-four arrangements of three items are still all different from each other. After some thought, I can more or less understand that this must be so. But it certainly brought me up short when he raised the idea.
Extended Clinical Interviewing
Now I want to move, with one last example, to develop the idea of a kind of research that such a view of teaching and learning leads to and calls for: extended clinical interviewing. Early in my work in education I found that the Piagetian methods I used to investigate learners' understanding—that is, having them take their own understanding seriously, pursue their own questions, and struggle through their own conflicts—was at the same time a way of engaging people in pursuing their own learning. People became avid learners, even in fields which had not interested them before, and my ways of trying to follow their thoughts were, in fact, excellent ways to help them learn.
Later I came to realize that the circle is full: This way of helping people learn is at the same time an important form of research about how people's ideas develop. It really amounts to Piaget's clinical interviewing, extended in two ways: It can be extended over time, and it can be carried out with more than one person at a time.
This approach requires, however, more than just an interviewer's questions. Many of the interviews in Piaget's early books used only the interviewee's previous experience as the basis of discussion (What makes the wind? Where are thoughts located?). In contrast, the questions that I found most often engaged interviewees in the pursuit of their own learning grew from Piaget's later work, where children tried to explain or predict or describe relationships in something that they had before them and could transform or otherwise keep returning to (the last example above is based on an investigation in Piaget and Inhelder, 1951/1975). The more surprises people encountered, and the more possibilities they became aware of, the more they wanted to continue to do and to think.
Extended clinical interviewing as a research approach requires just as much resourcefulness in finding appropriate materials, questions, and activities as any good curriculum development does. Whether it be poems, mathematical situations, historical documents, liquids, or music, our offerings must provide some accessible entry points, must present the subject matter from different angles, elicit different responses from different learners, open a variety of paths for exploration, engender conflicts, and provide surprises; we must encourage learners to open out beyond themselves, and help them realize that there are other points of view yet to be uncovered—that they have not yet exhausted the thoughts they might have about this matter.
Only if people are interested, learning, and expanding their views does one learn anything about how people's ideas actually develop. Curriculum development goes hand in hand with following the intricacies of the development of ideas. (This intertwined relationship led me first to refer to this research as "teaching-research," 1987.)
Once we are willing to accept the real complexities of subject matter, we find that they lurk even in the most unlikely places. One of the abilities I seek to develop in teachers is the ability to recognize unsuspected complexities in what seems like straightforward, even elementary, material. (David Hawkins, 1978, has pointed out how mistaken it is to think that "elementary" ideas are necessarily simple.) It is always in confronting such complexities that one develops real understanding.
"And That's How They Did the Latitude Lines" . . .
"It Makes Me Dizzy"
I want to close with one detailed example of extended clinical interviewing that shows what can happen when learners confront, rather than cover, complexities. I want to show the process as it actually takes place in a group over time. I hope to be able to convey the relationships—both interpersonal and ideational—that this approach to learning entails. I hope to reveal the interplay of thoughts and feelings, the tantalizing confusions, the tortuous development of new insights, and the crowning accomplishment possible when people struggle honestly with their own ideas. I think it is a rare picture of minds at work.
This account involves a group of adults that spent eleven years pursuing a study of the habits of the moon. This group began at Massachusetts Institute of Technology as the Experiment in Teacher Development (Bamberger et al., 1981). After the official end of the two-year project, about ten of the original fifteen teachers wanted to keep going. We met periodically through a third year, as we tried to decide which strands of our work together we wanted to continue. For six of the teachers, moon-watching was really the most passionate interest. This was the experience that they felt had given them the greatest insights into themselves and their students as learners, and thus into themselves as teachers. (For more on moon-watching, see DiSchino, 1987, and Duckworth, 1986a.) So, for the last eight years, seven of us have continued to meet with a focus on moon-watching.3 There have been no dropouts. We meet for a two-day study session every summer, for one or two all-day study sessions during the year, and for evening meetings about once a month. By now, the teachers are familiar with most of my thoughts on the motions of the moon, and I am a learner like everybody else. This, in fact, does not change my role very much. In all of my extended clinical interviewing I keep asking people to say what they mean again, please, more clearly. In this group I have no special standing in asking for such clarification.
I did not set up the conflict described below. It emerged on its own as we continued to try to understand the motions of the bodies in our solar system. I may have played a role in keeping the conflict on the floor as an issue worth trying to resolve, and in refusing to believe too readily that we had resolved it. The discussion presented here is about what "east" means, which at first blush seems like a pretty simple idea. Let me first try to present two different views, and then give some sense of the discussion that took place.
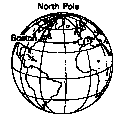
Both views put east in the general direction of the rising sun. ("Orient"ing literally means taking a bearing to the east, heading for the rising sun.) The first view is relatively simple: east is along a latitude, in the general direction of where the sun rises. The second view is more difficult to convey, and for us it came from two different sets of thoughts. The simpler of these is the following. East lies 90 degrees from north, in the general direction of the rising sun. If you look at the North Star (or to the earth underneath the North Star) and put your right arm out at a right angle, you'll point east. If you cut a 90-degree L-shape from a piece of paper, and lay it on a globe so that one tip of it is at the North Pole and the bend in the L is at Boston, then the arm that is heading east does not go along a latitude; it goes on a gentle slant from the latitude, so it ends up crossing the equator.
North Pole
Our second way of getting to this view is the following. In September you may find the sun rising in a certain position, relative to your house, for instance, or to the end of your street. As the months go by the sunrise point changes, moving to the right along the horizon, until by Christmas it is very much further to the right. By mid-January it has started to move back, until some time in March it is again where it was in September; it then continues to move to the left for a couple of months. In June it begins to move to the right again, and by September it is back where it started. So where; in all this, is east? This group thought of the one in the middle of those extremes as a reasonable candidate—the place where it started in September and that it reached again in March. That is also the time when the sunrise and sunset divide the twenty-four hour period into exactly half. Everywhere in the world, that day, the twenty-four hour period is going to be divided exactly in half. Everyone in the world, that day, will look to the sunrise to find where the exact east is. And here's what that led us to think: If everyone on one north-south line from the North Pole to the South Pole is looking toward the sun at the same sunrise moment, they are all looking at the same place at the same moment. On that day, the sun is actually rising so as to keep going directly overhead at the equator, which means that we must all be looking, not directly along a latitude, but in a direction gently sloping towards the equator.
So we had two reasons to think of east as tending toward the equator, rather than along a latitude parallel to the equator. And, of course, we also had commonsense and pragmatic reasons to think of east as heading along a latitude. In order to proceed with an investigation that we were engaged in, we needed to know which of these easts to deal with.
This discussion lasted three long sessions, which are the essence of the following account. The first took place at one of our two-day summer retreats, in June 1987. It refers back to a conversation at a retreat three years earlier, when one central idea first emerged and left us perplexed. The second session took place in December at an all-day meeting, and then there is a follow-up to that. Much material has been cut, but I still hope to convey a sense of the nature of what can happen when complexity is accepted as a pedagogical resource, rather than avoided.
Fern: [one major protagonist in this discussion, always willing to take on a seemingly unlikely idea if it expands her/our understanding]. . . [T]here's always east, even if the sun isn't rising there. There's still due east . . . it's down there, because it's towards the equator.
Wendy: [another major protagonist] No. I'm not happy with that sentence, I'm sorry. Due east is not towards the equator. . .
Fern: Where is due east, even if the sun isn't there? It's towards where the sun rises on the equinox, which is ... towards the equator ....
Wendy: What makes you think that it tips towards the equator? . . .
Eleanor: [altogether quite unsure of myself in the discussion] It's the 90-degree thing [the L-shape, which we had discussed earlier]-the latitudes are not 90 degrees to the longitudes....
Wendy: I think I see what you're saying. You're saying that if I look due east eventually my eyes will . . . touch the equator . . .—if I could look around the corner.
Fern: You know what it is? There's always due east. Whether or not the sun rises there. And what due east is, the definition of it is, where the sun rises on the equinox. I think of it very differently. I think of due east as, I drew a line from the North Pole to the South Pole and then went 90 degrees off . . . from that.
Eleanor: OK, that would come to the same thing....
Wendy: But I don't like it.... I don't like it ending up on the equator.... It really makes me nervous....
Wendy: [taking a styrofoam ball] Well if I draw a line from there [A—point standing for the North Pole] to there [B—point standing for Boston] and go at a right angle [she starts to draw a line like a latitude]—
Fern: Nope, that's not a right angle, your right angle's going to go like that [tending toward the equator].
Wendy Yeah, but I don't like that right angle. I'm having serious problems with that right angle.... Well how come the latitudes don't tilt down? How come they don't bump into the equator?
Fern: Latitudes are latitudes, they're not east.
Wendy: You say Spain is due east from of us, and—
Eleanor: That's a good point....
Wendy: If I get into a boat and I drive due east and I keep the compass on due east, I bump into Spain.
Fern: [stretching things a bit] You say Spain is on the same latitude, you don't say Spain is due east.
Eleanor: [quite uncertain] Although we do say that....
Fern: They're not east-west lines, they're latitudes. If they were east-west lines we wouldn't need latitudes.
Eleanor: Huh?
Mary Rizzato: Why? Why [then] do you have longitudes? They're [after all] north-south lines.
Jinny: [laughing] That was a little—cryptic! Go on!
Mary R.: Go on, we need to hear this.
[We all recognized that she had made a far-out comment, but had confidence that Fern would say something interesting about it.]
Fern: OK, here we go. [Fern thought silently for a while but to our great disappointment, she decided she did not, after all, have something clear to say.] No...
Wendy: Alright, hang on. You're saying that if I got a compass, and I started walking in California, and I followed that compass wherever it said east, I would end up on the equator.
Fern: Right....
Wendy: You're saying that if I were a sailor, and my compass told me to sail due east, I would end up on the equator no matter what I did.
Fern: Right...
Mary R.: So which way would you have to go to get to Spain?
Jinny: You'd have to go—
Mary DiSchino: North of east....
[with hilarity]
So north isn't north and east isn't east....
So if you want to stay
in the Northern Hemisphere you have to keep going north.
Wendy: [arm around Fern's shoulder] This is the first time in eight years that I don't understand what you're saying. In eight years you're the only person who I've always, always understood....
If I'm driving [east] . . . am I driving [on a latitude]?
Jinny: Probably if it's short enough. Because, right? it's going to take you a long time to get down to the equator. [This was the first inkling of a resolution—but nobody noticed. ]
Mary R.: It's incredible. Well it's interesting, one of the kids last year in mapping asked me why there was an Eastern and a Western Hemisphere. Why did one get named one and the other one get named something else [given that they each get their turn at sunrise]. [She laughs.] I said, "I have no idea." I had no idea. I mean, why? . . .
Mary D.: What would happen if we took the crust off the earth and then started walking due east? . . . Lie it flat . . . It would be like the orange peels [another reference to an earlier session]....
Wendy: Do you mean to say you don't believe that compasses tell you where due east is?
Fern: No, I do.
Wendy: So you think that if I were a sailor and I sailed whatever number of degrees due east is, 90 or whatever, that I would end up on the equator? [We acknowledge the need to adjust a compass for magnetic north, and proceed on the assumption that that is done.]. . .
Fern: I think you'd go due east.
Wendy: And would you end up on the equator?
Fern: Yeah.
Eleanor: Instead of Spain
Wendy: Instead of Spain. If Kevin, who has sailed and navigated, said that doesn't happen, would you say your due east is different from the compass due east? I don't know what he's gonna say, he might say, yes, you have to correct— . . .
Fern: This is the thing. This is the thing. I think maybe this is the thing. If you start—
Now here, Fern is able to articulate her insight, and it is related to Jinny's partially formed thought above. She comes to it, however, alas, just as the men and children arrive back for lunch, so the tape is stopped. I wrote down the following, in which Fern refers to an example we had used of walking along the 49th parallel.
Fern: If you walk east, you walk along the [US-Canadian] border; if you look east, you look into the United States.
We get a brief respite from the children, to finish our discussion, and the tape is back on. I had not understood what Fern had said, and Jinny tries to recapture it for me.
Jinny: . . . Where were we. We were on the border. If you're going to walk, umm, if they, if you continue to adjust— . . . 90 degrees, so you stay consistently 90 degrees east of north, you know, 90 degrees in relationship to north, you'll stay on that border, and . . . [a new thought she has here now] and that's the definition of a latitude....
Eleanor: But I want to know, I just want to know the thing you said, about it keeps pushing up; could you say that part again?
Mary R.: Well it, it keeps, if you're just walking, [Eleanor: Yeah.] then you're just, you're constantly straying down. [Eleanor: Yeah.] But if, if you, if you keep yourself on the compass, and you constantly push the compass, then you're constantly keeping yourself at 90 degrees . . .
Eleanor: And what's the pushing up? . . .
Jinny: You have to adjust. You have to keep the adjustment happening. Because of. . . the sphere. That's what the pushing up is . . .
Eleanor: Yeah. I haven't quite got that. I'll keep thinking about it.
[In December, we started by watching some of the summer's videotape, and then the conversation went on this way.]
Joanne: [Who had been running the videocamera in the summer session] The last thing you said there [on the tape], do you know what it is? "There's always due east." [laughter]
Fern: [reflecting on her insight at the end of the last session] I think where we ended up was if you navigate, if you're a sailor and you navigate and you're heading due east, you don't go to the equator. You go to Spain or whatever—
Eleanor: Any step is headed toward the equator, but the next step— . . .
Mary D.: It's due east from that step. Due east is due east from each step that you take. That's how you get across [to Spain]. As opposed to due east from your starting point. [Jinny: Mmmm.] If you look at a compass when you begin, and you go due east, if that compass froze there at that moment, then you'd get to the equator, but the compass is heading due east even when you're ten steps ahead of where you started
Mary R.: It corrects it sort of.
[I still do not follow the line of argument, and keep asking for more clarification.] . . .
[Fern starts drawing a picture.]
Wendy: If you were walking around a circle, around the top of the globe . . . It's telling you to go, like, due east is this way [she steps slightly outside the circle]. But really it's saying take a step this way and then it says, OK, now, north is over there.
[Wendy essentially outlines the argument that I finally understand a little later. I shall present it more clearly at that point.]
Jinny: It's like making a circle in Logo . . .
Wendy: East is pointing off the circle, down.
Eleanor: Yeah. But I don't believe it. I believe it but I don't get it. You get it and you don't believe it...
Jinny: Well the only thing I said, just when Wendy just did that, is it's like making a circle in Logo
Mary R.: With straight lines. You make a circle with straight lines.
Wendy: That's lovely.
[I try but fail to understand this analogy.] . . .
Mary D.:. . . You keep moving, also. That's part of it.
Fern: [She finishes her drawing.] Something like that picture, ...
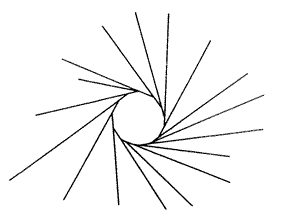
Eleanor: How come I go there [around the circle] when the compass says to go of into space, I don't know. How come I go there, that's my question. [Jinny and Eleanor laugh.]
Wendy: 'Cause the circle is big enough that you can take a step this w—I mean if you think of, like, octagons, but with, like hundredsagons . . . You walk a little bit this way, and then you look and say, oh, north has moved from here to here, 'cause I've gone a little bit around . .
Eleanor: 'Cause north moves.
Mary R.: It doesn't.
Eleanor: No, it does, with respect to me.
Wendy: Perhaps you move with respect to it.
Mary R.: Yeah.
Eleanor: Yeah. [I start walking with my left arm out to the side, supposedly pointing at the North Pole, and my right arm straight ahead of me, supposedly in the direction that my compass would indicate is east] So I take this step now .
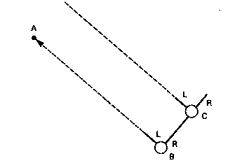
A—point standing for North Pole
B—my starting position
C—my position after one step
L—my left arm
R—my right arm
[ahead of me essentially down one of Fern's lines] but I can't have . . . kept my hands like that, . . . 'cause I have to stay like this . .
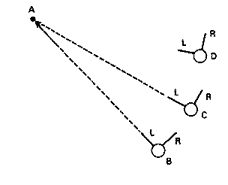
A—point standing for North Pole
B—my starting position
C—my position after one step
D—my position after 2nd step
L and R—positions of my arms
[I shift slightly left, so my left arm still points to a supposed North Pole.] So then I take this step here [down another of Fern's lines], and then I have to move back [to the left] like that, [Mary R.: Right, right.] and then I take this step here [down another line]. [The others break out in applause.] . . . And then I follow that one [another line], but if I take my left arm with me, it's left the North Pole, and it has to correct back again. . .
Mary R.: It keeps adjusting you. It's really neat. . .
Wendy: But if you glued, if you could clamp the compass so it wouldn't move when you walk a little bit, suddenly north would be at a totally different place....
Fern: . . .[T]his line that you're going around here is the latitude . . . that would bring you to Spain, as opposed to down there [down one of the line] to the equator. . . . This shape, when you put this shape onto the globe [her drawing, with the North Pole at the center], this line [the circle] would set at a certain latitude, . . .
Mary R.: Everything else would go down. . .
Fern: 'Course then they would keep going past the equator, I don't know about that.
[This introduces the third idea of east, which we did not resolve with the other two. The going-to-the-equator view of what east is had, as you will recall, two sources. The L-shape crosses the equator, while in the other version, Fern's lines would wrap around the equator.] include a short bit of discussion of that idea...
Fern: [T]here's something wrong about the L, maybe . . . maybe it's not really an L ...
Eleanor: Wouldn't it stay on the equator once it got to the equator? . . .
Mary D.: Because then if you're in the Southern Hemisphere, you'd do the opposite. .
Joanne: What kind of a shape is that?
Eleanor: That is an amazing shape, though—a spiral that then reaches a circle and stops getting bigger.
Fern: The only way you'd get this line [the one that would wrap around the equator] is if you had a laser beam, and you shot your laser beam from where you were standing, due east, and in an instant, the laser beam burns a trail on that line....
Joanne: This line is a continuation of one of those lines up there [in Fern's drawing], which eventually reaches the equator....
Wendy: If you could stand on the earth, on the equinox, and shoot one of those pistols that has a string with a sucker, and you could shoot it right at the sun . . . and have it "blip" on the sun, so you had this lovely string from you to the sun. And then the earth began to turn, that day, and the string would be wound—. . .
Mary D.: You could be putting this dot on the earth, as every point on the earth passes through sunrise. This is sunrise. As it passes through sunrise, if there were something spitting at the planet, making points on it, . . . when you went through, when the day was over, you'd have an equator on your planet . . . I see how the equator is made. Now the equator has a different meaning for me.
[We return to a discussion of our other two easts.]
Wendy: I will not agree that that's due east, toward the equator.... I want an-other word than due east for that....
Wendy: [If Fern's east is east] how can you say Spain is east of us? Spain is north of us [since the compass reading is corrected to the north].
Mary R.: No it's not! .
Wendy: But you have to constantly correct, after each step.
Mary R.: You don't have to correct, because your constant corrects for you. Either the north star, or the compass—one of those change for you. They keep you going in the direction, and that's how you, and that's how they did the latitude lines.
Wendy: But then, why—Then there are two easts.
Mary D.: Yes! We said that. There's Fern's east, and there's the latitude east.
Wendy: Right. But I don't—, I can't—, I don't feel comfortable with it . . . it makes me dizzy....
Wendy: What I would like to do is . . . I'd like to present that kind of information to somebody who deals with east and west....
Fern: I'm thinking, if he came in here right now, and said, you're right and I'm wrong, I would think he hadn't thought about this problem long enough....
Wendy: . . . Now we have two different words for east.
Eleanor: Different meanings for east.
Wendy: Right. And one word.
Jinny: In two different lang—I mean it's like two different worlds, it's a flat world and a spherical world....
Eleanor: You'd like a map-maker.
Wendy: Yeah, or somebody who sails....
Fern: I don't think any of those people would have had to resolve this issue in order to be able to do what they do....
Wendy: ... What I understood today doesn't fit with what I've understood from all of that learning and all the things that I understand about east so far. Or believe about east, have read about east, hold about east . . . I'm trying to think if there's another way to resolve it that wouldn't have two easts.
Fern: The two views that we have right now are not, one, that east is Spain and the other one that east is something else. We have two views. One is that east is Spain. And the other is that east is both Spain and something else.... They're not two conflicting things. One is part of the other.... Do you know what I mean? Like one has more parts to the explanation, . . .
Wendy: I don't think that anyone will agree-
Mary D.: Then why aren't we the experts?
We did go off to see Philip and Phylis Morrison, creators of PBS's The Ring of Truth, which included one episode on map-making. And there we learned, to our extraordinary satisfaction, how Charles Mason, astronomer, and Jeremiah Dixon, mathematician and surveyor, laid out the Mason-Dixon line. At night they fixed north, by the stars By day they cut through the trees at 90 degrees from north. At night, they fixed north again, and when they started each new day, returning, in Jinny's terms, to the "flat world," they had to adjust their continuing swath slightly to the north. It was just like Wendy's walking circle. As Mary R. had said, "And that's how they did the latitude lines."
Conclusion
This is an exceptional group, admittedly; not in its make-up at the outset, but in its history of learning together. That is one reason I wanted to present an impression of their work together. They know it pays off to stick with a complex issue. They know the value to each person of starting from her own set of ideas and points of engagement and relating new ideas to that base—Piaget's fundamental point, but so rarely really acted on in formal education. And they know the value of paying attention to each other's ideas, to see how they can expand their own through making the accommodations necessary to assimilate other points of view—classic Piaget again.
Any one of us in this group might have dismissed the discussion by saying that, of course, Spain is east, so let's get on with it. Or, well, we know that east is where the sun rises, so let's get on with it. Instead, by recognizing that this was a complex issue, we pushed our ideas into a construction of a fairly sophisticated understanding of relationships between a flat world and a round world. This took us into map-making, surveying, history, geography (as we talked about this issue with various people we learned that the east-west highways in the Canadian prairies have periodic small-angle turns—like Wendy's hundredsagons—having been set out in a fashion similar to the Mason-Dixon line, and math (what is the mathematical nature of that third version of east, a curve which approaches the equator and wraps around it?).
Our delving into these areas grew out of the simple question of what east is, which itself grew out of the simple question of what can we see the moon do in the sky—a question that has engaged this group for eleven years. This exaggerated example is the strongest way to make my point: Most areas of study that are at all worth our attention entail far more complexity than is acknowledged in our curriculum; and, further, people's intellectual engagement, when they are given the chance to pursue these complexities according to their own lights, is extraordinary. Our challenge as curriculum developers is to find the ways to engage learners, young or old, in the complexities of the areas we think it is important for them to know about. As researchers who are interested in how ideas actually develop, I think we have exactly the same challenge. I hope I have made clear how intertwined these challenges are.
I am under no illusion that, in the current climate of oversimplification, curriculum activity that celebrates the complexities of subject matter will be readily received. The point of this article is to rail against that climate, and to offer an idea of what our schools, our teachers, and our students may be missing by being subjected to that oversimplified view of the nature of teaching and learning.
I would like to end with some high school students' points of view, that poignantly express their awareness of how they are short-changed by current curriculum. With Candace Julyan (1988), they studied trees changing color in the fall.
They were watching the trees themselves, in all their complexity, and trying to relate what they saw to their textbook course on chlorophyll and photosynthesis. The quotes exemplify their feelings about details that make a complex study accessible; about being able to figure out complex things in their own ways; and about the futility of trying to over-simplify curriculum.
It took me a while to get it . . . [to get] all my ideas together and see what I think. Once I got it [it] was good . . This is fun. I like it. It's neat that I figured all this out.
I was thinking how the wind takes the tree and the leaves . . . and when the tree bends, it stops feeding the leaves. Did you ever think of that?
I love this project . . . I can never come up with ideas like this during labs . . . But this, it seems like I can come up with ideas really well. I don't know. I like this so much. I love it . . .
You have to think. I don't think a lot of people like to think . . . [This study] takes a lot of figuring out. It's fun, but it's hard.
. . . They throw something new at me and I can't stand it, and I have to do it their way. That's what I don't like about science, everything has already been figured out ahead of time. But if you find something different it's wrong.
I don't know why we read about trees in science class. It seems stupid not to come outside and really study 'em, don'tcha think?
References
Bamberger, J., Duckworth, E., & Lampert, M. (1981). An experiment in teacher development. Final report (Contract No. B-81-0042). Washington, DC: National Institute of Education.
DiSchino, M. (1987). The many phases of growth. The Journal of Teaching and Learning, 1(3), 12-28.
Duckworth, E. (1964). Floating color tubes. Nature and Children, 1(2), 6-7.
Duckworth, E. (1986). Inventing density. Grand Forks, ND: North Dakota Study Group On Evaluation.
Duckworth, E. (1987). "The having of wonderful ideas" and other essays on teaching and learning. New York: Teacher's College Press.
Elementary Science Study. (1967a). Gases and "airs." St. Louis: McGraw-Hill.
Elementary Science Study. (1967b). Senior balancing. St. Louis: McGraw-Hill.
Hawkins, D. (1978). Critical barriers to science learning. Outlook, 29, 3-23.
Julyan, C. (1988). Understanding trees: Four case studies. Unpublished doctoral dissertation, Harvard University.
Piaget, J., & Inhelder, B. (1975). The origin of the idea of chance in children (L. Leake, Jr., P. Burrell, H. Fishbein, Trans.). New York: W. W. Norton. (Original work published 1951)
Schneier, L. (1990). Why not just say it? Unpublished manuscript. Harvard Graduate School of Education.
1. From The Poetry of Robert Frost edited by Edward Connery Lathem. Copyright 1936 by Robert Frost Copyright © 1964 by Lesley Frost Ballantine. Copyright © 1969 by Holt, Rinehart and Winston Reprinted by permission of Henry Holt and Company, Inc.
2. For an analysis of one high school student's developing understanding of this poem, see Schneier, 1990.
3. The members of the group besides myself are: Jinny Chalmers, Eliot Pearson Children's School, Tufts University. Medford, MA; Joanne Cleary, Tobin Elementary School, Cambridge, MA; Mary DiSchino, Graham and Parks Elementary School Cambridge; Fern Fisher, Workman's Circle School. Brookline, MA; Wendy Postlethwaite, Consultant; Mary Rizzuto, Graham and Parks, Cambridge.